If you are new to Machine learning, the concepts of gradient descent might be a bit too advanced, so let’s start from the basics and work our way up. Machine learning mostly involves predicting an output based on your given input. The input can be an area in sqft of a property to predict the price of the property, the size of the tumour to predict if it is malignant or not, image of an animal to predict if Cat or a Dog. Literally in any problem that involves using machine learning algorithms to predict something, there’s always an input and an output.
Now that this is clear, let’s take it a step further. How does the machine make its prediction? There must be some kind of defined system, that uses all the data to come up with that output prediction you receive in the end.
There is one, and it’s a mathematical function, just like any other simple mathematical function you can imagine. Say the price of a house is 10 times its area in sqft, you can easily represent this as a function of x (area of the house).
Of course, this is a hypothetical case with a very impractical function, but when it comes to supervised machine learning, it’s all about the machine finding the right equation based on the input data that are fed into it.
PURPOSE OF LINEAR REGRESSION
Now you might be wondering where does linear regression come in? Let’s take a scatter plot of housing price vs area data. On this chart, we plot the x and y coordinates for 13 houses, just to look at the trend between the area and the price.
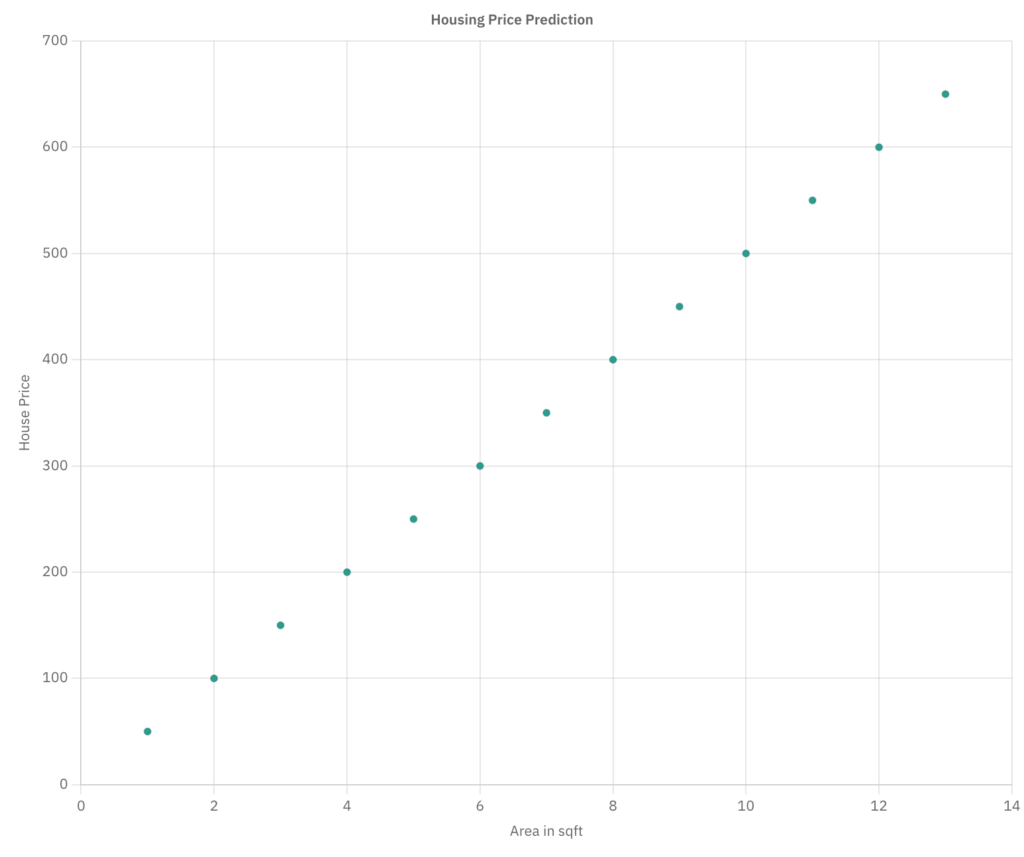
Nothing complicated, we can tell the Housing Price (y) is 50 times the area in sqft, and you can simply create an equation that can help you predict the housing price for a sample that isn’t present on this graph, this is called a Model Function.
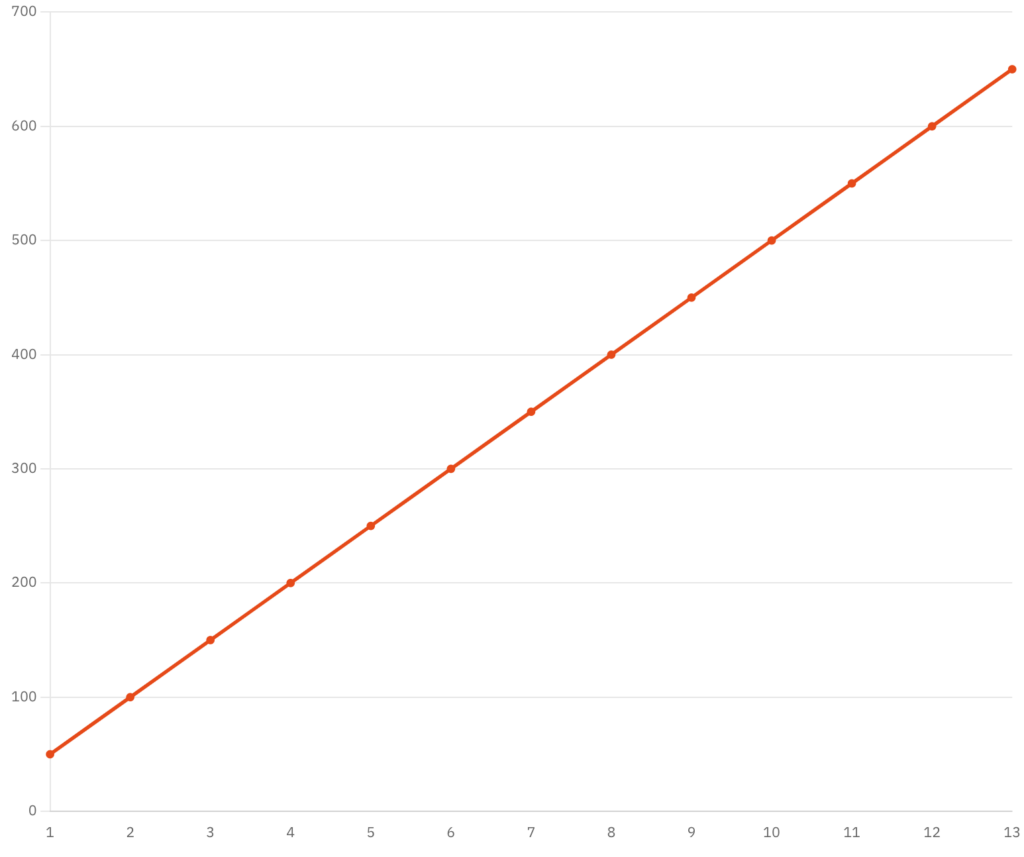
Say you find a house for 8.2 square feet (a hamster house more like, but bear with me for simplicity), based on the previous trend (price being 50 times the area), we can say the house is going to cost $410, even though we did not find a sample with an area of 8.2 sqft in our scatter plot.
This is exactly what happens in supervised machine learning, you find the best line (line of best fit) for the input data that is already provided, this line’s equation is called the model function, which is directly used to predict the output y.
The question now becomes, how do we effectively build the program, that automatically finds this line, or in other words, the equation for the line that best fits this data, which we can then use for our predictions? This is where Linear regression comes into play.
LINEAR REGRESSION
Now that you know how the machine makes its predictions in supervised machine learning, it’s time to address the most important type of model when it comes to finding the linear relation between the input and the output features.
Linear regression helps us attain that function that gives the x → y mappings for our predictions. To do that, we first train our model with some data, which would be used to create our equation for the line of best fit. The dataset used to train the model is the training set, and similarly, the dataset you use to check if your model is doing well, in other words, to test your model, is called the test set.
There are some variables and representations that you must know in order to understand the breathtaking math you are about to see.
x = Input feature
y = Output variable
A training example is a row of data, or a point on the graph that contains the input features as well as the output variable. The variable “i” would be an index of the row, which can range from 0 (for the first row) to m(the last row).
A linear equation in a single variable (x in this case), can be represented using the weight(w), and the bias(b). You might remember them from high school as the slope(m) and the intercept(c), it’s the same thing.
So based on the weight and bias, you can find the value of y for a particular input value of x. Our task is the find the best values for w and b. Since we are looking for “the best” values for w and b, there must be some way to compare the values for w and b, and there is. This is called the Cost function, and it helps you to see where you stand for the values you pick for w and b.
COST FUNCTION
The cost function helps you find the “cost”, or in other words, the error that is produced by the equation for certain w and b values. In intuition, you put in the values for w and b into the function, along with a training example ( x(i) , y(i) ).
The cost function makes a prediction ŷ based on the given w and b values, and this prediction will be compared to the actual y value in the given training example. This is called the error, and we find this by finding the difference between the y value that we predicted, and the actual y value for that training row. This error value will then be squared, so we call it the Mean Squared Error(MSE).
Cost Function Formula (Squared Error Cost function)
The Cost function here, is J(w,b), as you can see, for each row in the training example, the index i goin from 0 to m (Index of the last row in the training set), we take the Mean Squared Error each time and sum it all up. Once we find this sum, we divide it by 2m. Although the cost function would work even without the (1/2m), but this is just to simplify the equation when we find the derivative of the function later.
THE GOAL WHEN USING COST FUNCTION ON LINEAR REGRESSION
When you take b=0, here, for each value of w you end up with a different point, once u get a graph for J(w), you need to pick the value for w that gives the smallest value when passed through the cost function, hence our goal would be to minimize J(w).
Similarly, when you have b along with w, you need to find the value for w and b that minimizes J(w,b). In intuition, this means, we must find a value for w and b, that gives us a line that has the least error (a lower cost value). The line that produces the least error would obviously be the line that best fits the data since our predictions in this case would be very close to the actual values. It should be apparent by now, how we use the cost function to assess how well our model does when it comes to predicting based on the training set (lower the cost, better the model).
VISUALIZATION OF COST FUNCTION IN LINEAR REGRESSION
We can visualize the cost function using a 3D plot, by plotting the variables w and b on the x and z axis, and the cost value we get when we pass w and b into the cost function (J(w,b)) on the y axis. As previously mentioned, our goal would be to minimize the cost function, and hence, the lowest point on the y-axis (Cost function) would be the minimum cost value we can get using any values for w and b. Our goal is to find the values for w and b at this minimum.
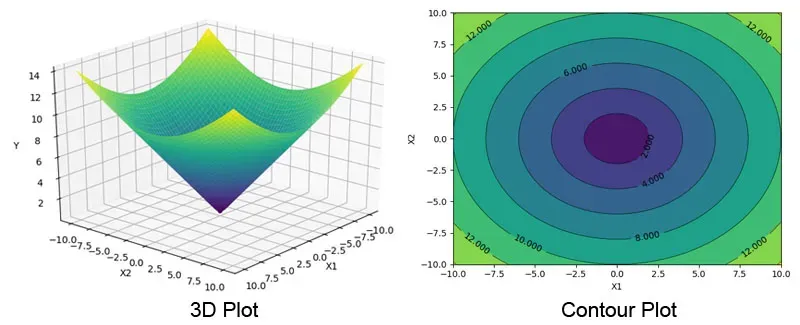
Of course, it’s easy for us to look at the 3D plot and find the w and b values at this point, but the cost function is always way more complicated than this. A mean squared error cost function always gives a hammock-shaped cost function, when you use an advanced neural network, you get something like an irregular surfaced graph. In such cases, we would need an algorithm to find this point for us. Once this point is found, the w and b values at this point would be the weight and bias we would need to use to get our line of best fit and we’d be good to make our predictions.
GRADIENT DESCENT
When we talked about the algorithm that we can use to minimize the cost function, that would be Gradient Descent. There are many kinds of gradient descent, and in this article, we will purely focus on whats called the Batch Gradient Descent.
Outline:
- Initially, you start with some values for w and b.
- Then, you keep changing w,b to gradually reduce J(w,b)
- Repeat until you settle at or near a minimum
ALGORITHM
From the current position you’re at, you look around and find the direction where if you move a small step, you can get down to the local minima, and then go that direction by learning rate α (α is the learning rate, depending on how big α is, the size of the steps on each step changes).
$$ w = w – α \frac{\partial }{\partial w} J(w,b) $$
The partial derivative in the formula used to update the values for w and b essentially has a value that is positive or negative, depending on the slope at that point, if the slope is positive, the partial derivate would have a positive value, and hence subtracting a positive value from w would let us move towards the left of the curve (downhill). Similarly, a negative slope would end up increasing the value of w, letting us move right off the curve(downhill in this case).
CHOOSING THE LEARNING RATE (α)
- When α is too small, you end up making a change that is too minuscule every time you make a change, and these steps can end up slowing down the algorithm.
- When α is too big, you end up making a change too big, that you might diverge out of the surface and never reach the minimum.
It’s always better to start with a small value for α, say 0.001, and work your way up testing for 0.005, 0.01 and so on, and see what learning rate works the best for you.
DERIVATION
This is not really something you must understand to work with gradient descent or linear regression, but if you are interested in the math behind it, feel free to take a look.
This type of gradient descent is known as Batch Gradient Descent. Meaning, each step of the gradient descent uses all the training examples.
VECTORIZATION
$$ f_w,_b (x) = w_1x_1 + w_2x_2 + w_3x_3 + … +b $$
As you’ve seen before, this is the formula we use for our prediction, which we can write as a vector for w. The w vector is going to store all the values for the weights for the features from 1 to n. This way, we can shorten our equation from multiplying a w value with its respective x to a dot product between the weights vector and input values vector.
On code for the summation of products, we will be iterating over the list from index 0 to n-1 while adding the respective product to f and finally adding b to the sum, giving us the prediction value for our function.
f = 0
for i in range(0,n):
f = f + w[i] * x[i]
f = f + b
Now that we have our vectorized equation, this task will get much easier than using the summation functions. This is because, with a vectorized equation, you wouldn’t have to loop through each index, and instead run your calculations in one go. This is much more efficient in terms of speed and computation.
On code, we make use of NumPy’s dot method to achieve the same.
f = np.dot(w,x) + b
GRADIENT DESCENT FOR MULTIPLE LINEAR REGRESSION
Gradient descent for linear regression with multiple variables is not that different from the one we use for models with 1 input feature. In this case, however, you must update the weights and bias for each feature from 1 to n.
SIMPLE LINEAR REGRESSION ALGORITHM
Repeat{
Simultaneously update for wj(j = 1→n) and b
} until convergence
MULTIPLE LINEAR REGRESSION
Repeat {
Simultaneously update for w_n(j = 1→n) and b
}
POLYNOMIAL REGRESSION
Polynomial regression is a form of regression that uses higher exponential powers on the variables to better fit the curve. On data where the x increases at an exponential rate for y, a linear function would result in underfitting.
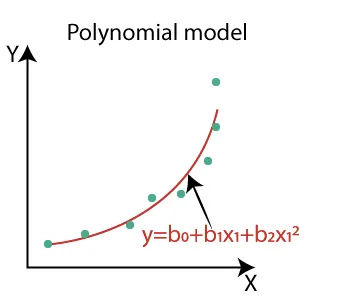
Gradient descent works the same, yet again, and like usual, you adjust variables and their exponents according to what fits the data best.
FEATURE SCALING
Say you have one feature that contains all the different values for the age of the house, which typically would be from the range 1-10. Say you have another feature that contains all the values for the area of the house in sqft, and this usually ranges anywhere in the thousands. When you train your model with such irregularities in the scale, you might end up training the model not so well. If you have different features with different scaling values, the contour plot ends up being squashed.
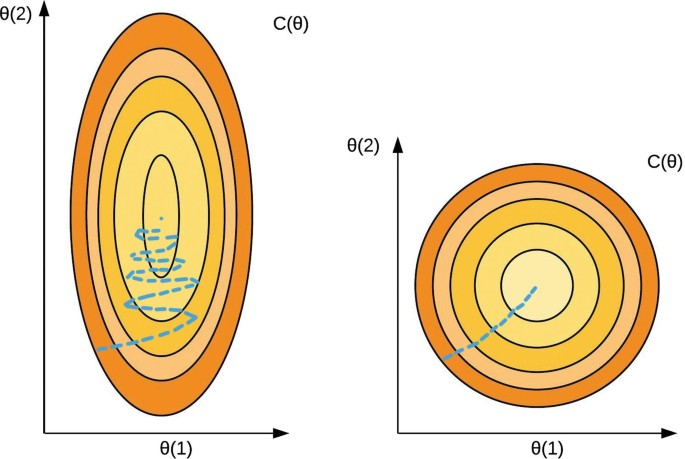
Take a look at the two contour plots above. The first plot is what you get when you run the algorithm on a dataset that has unscaled features. Unlike in the second plot, gradient descent tends to struggle on such a squashed plot. For this reason, we commonly use a few processes to implement feature scaling into our dataset. Let’s look at a few examples.
Mean Normalization
Mean normalization is one way of reducing the range of features close to the range of 0 to 1. We do this by subtracting the mean from the value and then dividing it by the range of the dataset.
and say,
With mean
This gives us a new scaled x1 value of
Z-score normalization
Z-score normalization is another common normalization technique to reduce all the values within the column to the range 0 to 1. This method of normalization is very similar to mean normalization, except instead of dividing the whole thing by its range, this time, you divide it by the standard deviation of all the values in the feature (σ)
WHEN TO USE FEATURE SCALING
The goal is to always get the values between -1 and 1 since this is the range gradient descent that works the best. Although it is fine to have a few values like 2 or -3, it’s best not to stray too far from this range. Meaning, values around -1 and +1 are fine, but values like 50 or 100, are a problem.
This is also the same for features that have values like -0.00001 or 0.00001 (even though they’re well between -1 and +1). These values are too small, and gradient descent does not work well on this range either. So it’s best to get them rescaled in this case too.
If you are not sure whether or not to use feature scaling on your dataset, it’s best to use it anyway. Mean normalization and Z-score normalization both do well in making sure your dataset is of the right scale to be sent for training your model.
HOW TO CHECK IF GRADIENT DESCENT WORKS?
Now that we’ve looked into gradient descent, and the best practices that you can implement to avoid slow and inaccurate training, it’s time to discuss a way to check if gradient descent worked on your model.
Firstly you would have to plot the cost function J(w,b) against the number of total iterations.
When the gradient descent is working properly on your model, you should see your cost value decreasing with an increase in iterations. If you don’t, that could mean there has been some mistake in ur implementation. If you see the cost value increasing rapidly with iteration, this could likely happen because your learning rate(α) was too big and gradient descent failed to converge, If the cost function increases at times, it means the learning rate is too high, in which case you must reduce α to a small value.
Let ε = 0.001, and if J(w,b) decreases by ε, you can declare convergence.
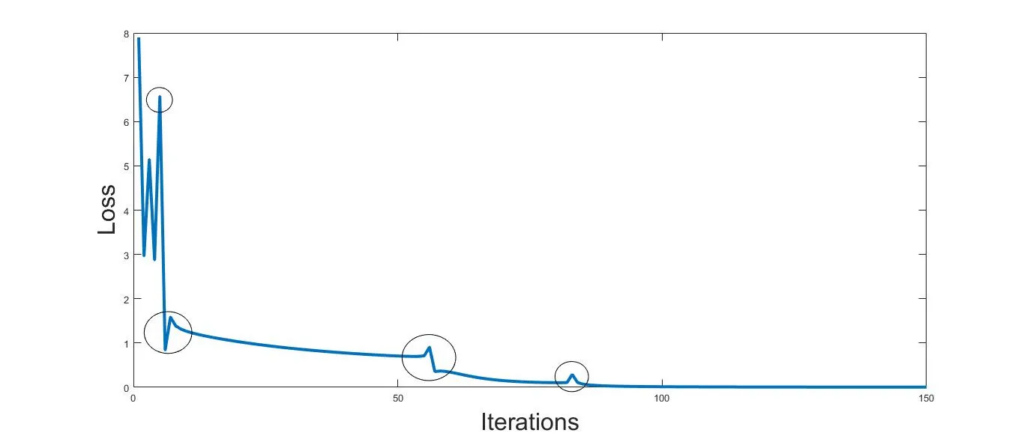
When picking a learning rate, you can pick a value like 0.001, then compare it with something like 0.01, and see what works for the model. If the graph looks wrong even on a small learning rate, it’s mostly because there is some bug in the model.

